Regular Polygon Calculator
Pentagon Shape
n=5
A 5 sided polygon
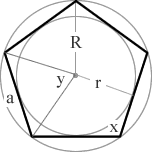
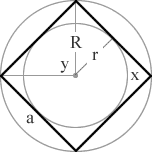
r = inradius (apothem)
R = circumradius
a = side length
n = number of sides
x = interior angle
y = exterior angle
A = area
P = perimeter
π = pi = 3.1415926535898
√ = square root
Calculator Use
Polygon Calculator
Use this calculator to calculate properties of a regular polygon. Enter any 1 variable plus the number of sides or the polygon name. Calculates side length, inradius (apothem), circumradius, area and perimeter. Calculate from an regular 3-gon up to a regular 1000-gon.
Units: Note that units of length are shown for convenience. They do not affect the calculations. The units are in place to give an indication of the order of the calculated results such as ft, ft2 or ft3. Any other base unit can be substituted.
Regular Polygon Formulas
A regular polygon is a polygon that is both equiangular and equilateral. All sides are equal length placed around a common center so that all angles between sides are also equal. When the number of sides, n, is equal to 3 it is an equilateral triangle and when n = 4 is is a square.
The following formulas were used to develop calculations for this calculator where a = side length, r = inradius (apothem), R = circumradius, A = area, P = perimeter, x = interior angle, y = exterior angle and n = number of sides.
- Side Length a
- a = 2r tan(π/n) = 2R sin(π/n)
- Inradius r
- r = (1/2)a cot(π/n) = R cos(π/n)
- Circumradius R
- R = (1/2) a csc(π/n) = r sec(π/n)
- Area A
- A = (1/4)na2 cot(π/n) = nr2 tan(π/n)
- Perimeter P
- P = na
- Interior Angle x
- x = ((n-2)π / n) radians = (((n-2)/n) x 180° ) degrees
- Exterior Angle y
- y = (2π / n) radians = (360° / n) degrees
-
Selected Polygons
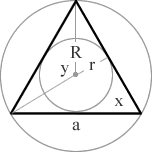
= 60°
= 120°
a 5 sided polygon

= 108°
= 72°
a 6 sided polygon
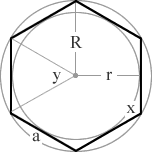
= 120°
= 60°
a 7 sided polygon
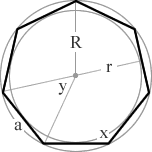
= 900°/7
= 128.57°
= 360°/7
= 51.43°
an 8 sided polygon
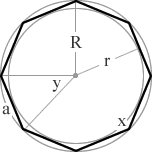
= 135°
= 45°
a 9 sided polygon
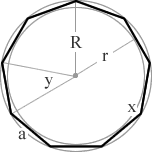
= 140°
= 40°
a 10 sided polygon
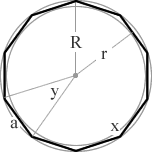
= 144°
= 36°
an 11 sided polygon
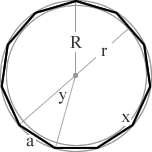
= 1620°/11
= 147.27°
= 360°/11
= 32.73°
a 12 sided polygon
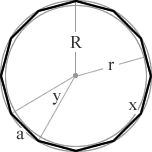
= 150°
= 30°
a 13 sided polygon
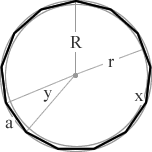
= 1980°/13
= 152.31°
= 360°/13
= 27.69°
a 14 sided polygon
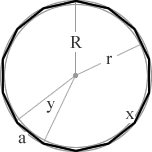
= 2160°/14
= 154.29°
= 360°/14
= 25.71°
References
Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 323, 2003.
Weisstein, Eric W. "Regular Polygon." From MathWorld--A Wolfram Web Resource. Regular Polygon.