Calculators

Geometry

Plane

Isosceles Triangle Shape

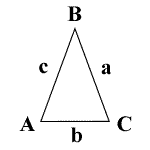
A = angle A
a = side a
B = angle B
b = side b
C = angle C
c = side c

A = C
a = c
ha = hc

K = area
P = perimeter

See Diagram Below:
ha = altitude of a
hb = altitude of b
hc = altitude of c

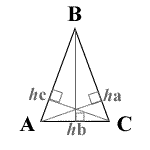
*Length units are for your reference only since the value of the resulting lengths will always be the same no matter what the units are.

Calculator Use

An isosceles triangle is a special case of a triangle where 2 sides, a and c, are equal and 2 angles, A and C, are equal.

In our calculations for a right triangle we only consider 2 known sides to calculate the other 7 unknowns. For example, if we know a and b we know c since c = a. Once we know sides a, b, and c we can calculate the perimeter = P, the semiperimeter = s, the area = K, and the altitudes: ha, hb, and hc. Let us know if you have any other suggestions!

Formulas and Calculations for an isosceles triangle:

• Sides of Isosceles Triangle: a = c
• Angles of Isosceles Triangle: A = C
• Altitudes of Isosceles Triangle: ha = hc
• Perimeter of Isosceles Triangle: P = a + b + c = 2a + b
• Semiperimeter of Isosceles Triangle: s = (a + b + c) / 2 = a + (b/2)
• Area of Isosceles Triangle: K = (b/4) * √(4a² - b²)
• Altitude a of Isosceles Triangle: ha = (b/2a) * √(4a² - b²)
• Altitude b of Isosceles Triangle: hb = (1/2) * √(4a² - b²)
• Altitude c of Isosceles Triangle: hc = (b/2a) * √(4a² - b²)

Calculation:
Given sides a and b find side c and the perimeter, semiperimeter, area and altitudes

• a and b are known; find c, P, s, K, ha, hb, and hc
• c = a
• P = 2a + b
• s = a + (b/2)
• K = (b/4) * √(4a² - b²)
• ha = (b/2a) * √(4a² - b²)
• hb = (1/2) * √(4a² - b²)
• hc = (b/2a) * √(4a² - b²)

For more information on right triangles see:

Weisstein, Eric W. "Isosceles Triangle." From MathWorld--A Wolfram Web Resource. Isosceles Triangle.