Cube Calculator x³ | x cubed
Calculator Use
Find the cubed value of a number n. Enter positive or negative whole numbers, decimal numbers or scientific E notation.
What is a Cubed Number?
Any number n with an exponent of 3 is written as n³. You pronounce it as "n cubed," or "n to the third power." To get the cube of a number multiply it by itself 3 times.
Therefore the cube formula is n³ = n × n × n.
What is a Perfect Cube?
A perfect cube results when you cube an integer, or a whole number without decimals or fractions. For example, 3 cubed is written as 3³ and 3³ = 3 × 3 × 3 = 27.
Since 3 is an integer, 27 is a perfect cube.
Imagine a block of smaller cubes 3 high, 3 wide, and 3 deep resembling a Rubik's Cube puzzle. Basically it's 3 sets of 9 blocks arranged in a 3 x 3 pattern. Since 3 x 3 is 9 which is also 3 squared or 32, you simply need to multiply by 3 again to get 3 cubed, 33 = 27.
It might help to picture any cubed number as a set of blocks. 103, or 10 cubed for example, would be a set of blocks 10 high, 10 wide and 10 deep. One face of the cube would have a set of 102 or 10 x 10 = 100 blocks. And 10 sets of those 100 blocks would be 10 x 100 = 1000 blocks.
10 × 10 × 10 = 10 × 102 = 10 × 100 = 103 = 1000
The image below is a large cube of 10³ = 1000 smaller cubes. Notice that each layer is 10 x 10 = 100 cubes.
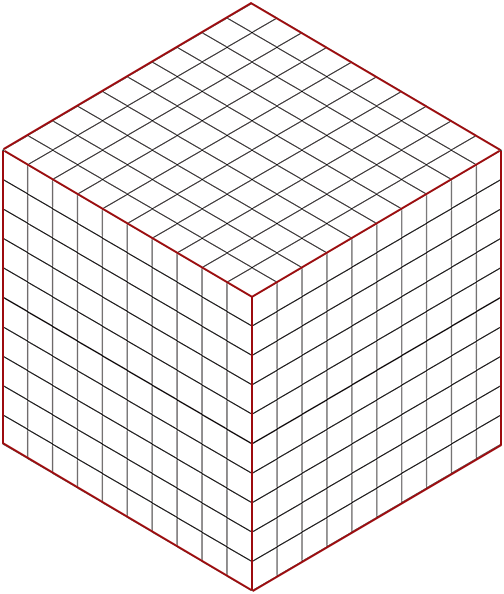
Numbers 0 through 10 cubed and the resulting perfect cubes
- 0 cubed is 0³ = 0 × 0 × 0 = 0
- 1 cubed is 1³ = 1 × 1 × 1 = 1
- 2 cubed is 2³ = 2 × 2 × 2 = 8
- 3 cubed is 3³ = 3 × 3 × 3 = 27
- 4 cubed is 4³ = 4 × 4 × 4 = 64
- 5 cubed is 5³ = 5 × 5 × 5 = 125
- 6 cubed is 6³ = 6 × 6 × 6 = 216
- 7 cubed is 7³ = 7 × 7 × 7 = 343
- 8 cubed is 8³ = 8 × 8 × 8 = 512
- 9 cubed is 9³ = 9 × 9 × 9 = 729
- 10 cubed is 10³ = 10 × 10 × 10 = 1000
See our List of the First 100 Perfect Cubes.
Cubing Negative Numbers
When you cube a negative number the result will always be a negative number. But it is important to understand how using parentheses affects the intepretation of the operation.
Putting a negative sign before the number or outside of parentheses means "take the negative of the number, cubed" as in
- -2³ means -(2 × 2 × 2) = -8
- -(2)³ means -(2 × 2 × 2) = -8
Putting a negative sign inside the parentheses means "cube the negative number," as in
- (-2)³ means (-2 × -2 × -2) = -8
You can see you'll always get a negative result with an odd exponent and a negative sign, whether it's inside or outside of parentheses. But when you have an even exponent the result depends on the interpretation of the negative sign and the presence of parentheses.
It may be helpful to use parentheses to clearly indicate which exponent calculation you intend. For example with even exponents and a negative sign the parentheses affect the result.
- -4² means -(4 × 4) = -16
- -(4)² means -(4 × 4) = -16
- (-4)² means (-4 × -4) = 16
You can see that the Square Calculator uses this strict interpretation. Without parentheses -4² means "the negative of 4²" which is -16.
Additional Reading
Wikipedia "Cube (algebra)" at https://en.wikipedia.org/wiki/Cube_(algebra)