Law of Sines Calculator

Basic Calculator

Calculators

Geometry

Plane

Law of Sines Calculator

Calculate:

Triangle Image

side a =

angle B =

side b =

Angle Units

Length Units*

Significant Figures

Answer:

Primary Equation:

\( A = \sin^{-1} \left[ \dfrac{a \sin B}{b} \right]\)

Sides:
a =
b =
c =

Angles:
A =
B =
C =

Other:
P =
s =
K =
r =
R =

Get a Widget for this Calculator

This Calculation Equation & Triangle

\( A = \sin^{-1} \left[ \dfrac{a \sin B}{b} \right]\)

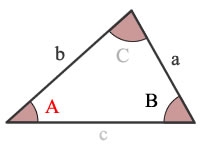
Triangle Diagram with Angles A, B and C and sides opposite those angles a, b and c respectively
A = angle A
B = angle B
C = angle C
a = side a
b = side b
c = side c
P = perimeter
s = semi-perimeter
K = area
r = radius of inscribed circle
R = radius of circumscribed circle

*Length units are for your reference-only since the value of the resulting lengths will always be the same no matter what the units are.

Calculator Use

Uses the law of sines to calculate unknown angles or sides of a triangle. In order to calculate the unknown values you must enter 3 known values.

Some calculation choices are redundant but are included anyway for exact letter designations.

Calculation Methods

To calculate any angle, A, B or C, say B, enter the opposite side b then another angle-side pair such as A and a or C and c. The performed calculations follow the side side angle (SSA) method and only use the law of sines to complete calculations for other unknowns.

To calculate any side, a, b or c, say b, enter the opposite angle B and then another angle-side pair such as A and a or C and c. The performed calculations follow the angle angle side (AAS) method and only use the law of sines to complete calculations for other unknowns.

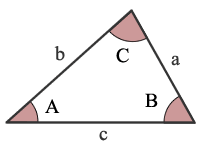
Law of Sines

If a, b and c are the lengths of the legs of a triangle opposite to the angles A, B and C respectively; then the law of sines states:

\( \dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} \)

Equations from Law of Sines solving for angles A, B, and C

\( A = \sin^{-1} \left[ \dfrac{a \sin B}{b} \right] \)

\( A = \sin^{-1} \left[ \dfrac{a \sin C}{c} \right] \)

\( B = \sin^{-1} \left[ \dfrac{b \sin A}{a} \right] \)

\( B = \sin^{-1} \left[ \dfrac{b \sin C}{c} \right] \)

\( C = \sin^{-1} \left[ \dfrac{c \sin A}{a} \right] \)

\( C = \sin^{-1} \left[ \dfrac{c \sin B}{b} \right] \)

Equations from Law of Sines solving for sides a, b, and c

\( a = \dfrac{b \sin A}{\sin B} \)

\( a = \dfrac{c \sin A}{\sin C} \)

\( b = \dfrac{a \sin B}{\sin A} \)

\( b = \dfrac{c \sin B}{\sin C} \)

\( c = \dfrac{a \sin C}{\sin A} \)

\( c = \dfrac{b \sin C}{\sin B} \)

Triangle Characteristics

Triangle perimeter, P = a + b + c

Triangle semi-perimeter, s = 0.5 * (a + b + c)

Triangle area, K = √[ s*(s-a)*(s-b)*(s-c)]

Radius of inscribed circle in the triangle, r = √[ (s-a)*(s-b)*(s-c) / s ]

Radius of circumscribed circle around triangle, R = (abc) / (4K)

References/ Further Reading

Weisstein, Eric W. "Law of Sines" From MathWorld-- A Wolfram Web Resource. Law of Sines.

Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 512, 2003.

http://hyperphysics.phy-astr.gsu.edu/hbase/lcos.html

http://hyperphysics.phy-astr.gsu.edu/hbase/lsin.html