Calculators > Geometry > Solid > Rectangular Prism Calculator

Rectangular Prism Calculator

Choose a Calculation:
h = m
l = m
w = m
Units*:
Significant Figures:
 
Answer:

l = m
w = m
h = m
d = m
S = m2
V = m3
| Share

Rectangular Prism Shape

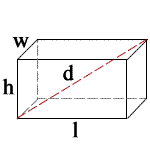
Rectangular Solid Diagram with l = length, h = height, w = width and d = diagonal

l = length
w = width
h = height
d = diagonal
S = surface area
V = volume

About this Calculator

Enter any 3 variables for a rectangular prism into this online calculator to calculate the other 3 unknown variables. A cube is a special case where l = w = h for a rectangular prism.

* Units: Note that units are shown for convenience but do not affect the calculations.  The units are in place to give an indication of the order of the results such as ft, ft2 or ft3.  For example, if you are starting with mm and you know r and h in mm, your calculations will result with s in mm, V in mm3, L in mm2, T in mm2, B in mm2 and A in mm2.

Formulas for a rectangular prism:

  • Volume of Rectangular Prism:
    • V = lwh
  • Surface Area of Rectangular Prism:
    • S = 2(lw + lh + wh)
  • Space Diagonal of Rectangular Prism: (similar to the distance between 2 points)
    • d = √(l2 + w2 + h2)

A cube is a special case where l = w = h.  So you can find the volume of a cube or surface area of a cube by setting these values equal to each other.

Calculations for a rectangular prism:

1. Given the length, width and height find the volume, surface area and diagonal of a rectangular prism

  • h, l and w are known; find V, S and d
  • V = lwh
  • S = 2(lw + lh + wh)
  • d = √(l2 + w2 + h2)

2. Given the surface area, length and width find the height, volume and diagonal of a rectangular prism

  • S, l and w are known; find h, V and d
  • h = (S - 2lw) / (2l + 2w)
  • V = lwh
  • d = √(l2 + w2 + h2)

3. Given the volume, length and width find the height, surface area, and diagonal of a rectangular prism

  • V, l and w are known; find h, S and d
  • h = V / lw
  • S = 2(lw + lh + wh)
  • d = √(l2 + w2 + h2)

4. Given the diagonal, length and width find the height, volume and surface area of a rectangular prism

  • d, l and w are known; find h, V and S
  • h = √(d2 - l2 - w2)
  • V = lwh
  • S = 2(lw + lh + wh)

For more information on cuboids see: Weisstein, Eric W. "Cuboid." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Cuboid.html