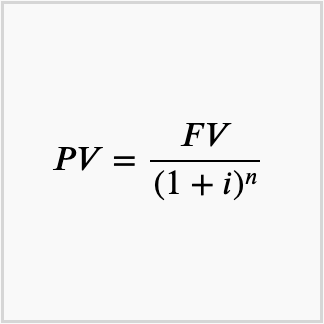Present Value Formula
Present Value and Annuity Formulas
Type
Formula
1 Present Value of a Lump Sum
\[ PV=\dfrac{FV}{(1+i)^n} \] PV = FV / (1 + i)n
2 Present Value of an Annuity
\[ PV=\dfrac{PMT}{i}\left[1-\dfrac{1}{(1+i)^n}\right](1+iT) \]
2.1 Present Value of an Ordinary Annuity
T = 0
T = 0
\[ PV=\dfrac{PMT}{i}\left[1-\dfrac{1}{(1+i)^n}\right] \]
2.2 Present Value of an Annuity Due
T = 1
T = 1
\[ PV=\dfrac{PMT}{i}\left[1-\dfrac{1}{(1+i)^n}\right](1+i) \]
3 Present Value of a Growing Annuity (g ≠ i)
T = 0 for an ordinary annuity
T = 1 for an annuity due
T = 0 for an ordinary annuity
T = 1 for an annuity due
\[ PV=\dfrac{PMT}{(i-g)}\left[1-\left(\dfrac{1+g}{1+i}\right)^n\right](1+iT) \]
4 Present Value of a Growing Annuity (g = i)
T = 0 for an ordinary annuity
T = 1 for an annuity due
T = 0 for an ordinary annuity
T = 1 for an annuity due
\[ PV=\dfrac{PMTn}{(1+i)}(1+iT) \]
5 Present Value of a Perpetuity
T = 0 for an ordinary annuity
T = 1 for an annuity due
T = 0 for an ordinary annuity
T = 1 for an annuity due
\[ PV=\dfrac{PMT}{i}(1+iT) \]
6 Present Value of a Growing Perpetuity (g < i)
T = 0 for an ordinary annuity
T = 1 for an annuity due
T = 0 for an ordinary annuity
T = 1 for an annuity due
\[ PV=\dfrac{PMT}{(i-g)}(1+iT) \]
7 Present Value of a Growing Perpetuity (g = i)
T = 0 for an ordinary annuity
T = 1 for an annuity due
T = 0 for an ordinary annuity
T = 1 for an annuity due
\[ PV=\dfrac{PMTn}{(1+i)}(1+iT)\rightarrow\infty \]
8 Present Value for Combined Future Value Sum and Cash Flow Annuity
\[ PV=\dfrac{FV}{(1+i)^n}+\dfrac{PMT}{i}\left[1-\dfrac{1}{(1+i)^n}\right](1+iT)\]
8.1 Present Value for Combined Future Value Sum with an Ordinary Annuity
T = 0
T = 0
\[ PV=\dfrac{FV}{(1+i)^n}+\dfrac{PMT}{i}\left[1-\dfrac{1}{(1+i)^n}\right]\]
8.2 Present Value for Combined Future Value Sum with an Annuity Due
T = 1
T = 1
\[ PV=\dfrac{FV}{(1+i)^n}+\dfrac{PMT}{i}\left[1-\dfrac{1}{(1+i)^n}\right](1+i)\]
9 Present Value for Combined Future Value Sum with Growing Annuity (g ≠ i)
\[ PV=\dfrac{FV}{(1+i)^n}+\dfrac{PMT}{(i-g)}\left[1-\left(\dfrac{1+g}{1+i}\right)^n\right](1+iT)\]
10 Present Value for Combined Future Value Sum with Growing Annuity (g = i)
\[ PV=\dfrac{FV}{(1+i)^n}+\dfrac{PMTn}{(1+i)}(1+iT)\]
11 Present Value for Combined Future Value Sum and Annuity including Compounding, Time and Rate
\[ PV=\dfrac{FV}{(1+\frac{r}{m})^{mt}}+\dfrac{PMT}{\frac{r}{m}}\left[1-\dfrac{1}{(1+\frac{r}{m})^{mt}}\right](1+(\frac{r}{m})T)\]
12 Present Value for Combined Future Value Sum and Annuity with Continuous Compounding (m → ∞)
\[ PV=\dfrac{FV}{e^{rt}}+\dfrac{PMT}{(e^r-1)}\left[1-\dfrac{1}{e^{rt}}\right](1+(e^r-1)T)\]
12.1 Present Value for Combined Future Value Sum and Ordinary Annuity with Continuous Compounding (m → ∞)
\[ PV=\dfrac{FV}{e^{rt}}+\dfrac{PMT}{(e^r-1)}\left[1-\dfrac{1}{e^{rt}}\right]\]
12.2 Present Value for Combined Future Value Sum and Annuity Due with Continuous Compounding (m → ∞)
\[ PV=\dfrac{FV}{e^{rt}}+\dfrac{PMT}{(e^r-1)}\left[1-\dfrac{1}{e^{rt}}\right]e^r\]
13 Present Value of a Growing Annuity (g ≠ i) and Continuous Compounding (m → ∞)
\[ PV=\dfrac{PMT}{e^{r}-(1+g)}\left[1-\dfrac{(1+g)^{n}}{e^{nr}}\right](1+(e^{r}-1)T)\]
14 Present Value of a Growing Annuity (g = i) and Continuous Compounding (m → ∞)
\[ PV=\dfrac{PMTn}{e^{r}}(1+(e^r-1)T)\]
15 Present Value of a Perpetuity (t → ∞) and Continuous Compounding (m → ∞)
\[ PV=\dfrac{PMT}{(e^r-1)}(1+(e^r-1)T)\]
16 Present Value of a Growing Perpetuity (g < i) (t → ∞) and Continuous Compounding (m → ∞)
\[ PV=\dfrac{PMT}{e^{r}-(1+g)}(1+(e^{r}-1)T)\]
17 Present Value of a Growing Perpetuity (g = i) (t → ∞) and Continuous Compounding (m → ∞)
\[ PV=\dfrac{PMTn}{e^{r}}(1+(e^r-1)T)\rightarrow\infty\]
- PV = Present Value
- FV = Future Value
- PMT = Payment Amount
- i = interest rate per period (decimal form)
- n = number of periods when compounding is once per period
- n = mt when compounding frequency is different than period frequency
- m = compounding frequency per period
- t = number of periods
- g = interest rate growth per period (decimal form)
- T = Type
- T = 0 for Ordinary Annuity (end)
- T = 1 for Annuity Due (beginning)
- r = interest rate per period in decimal form
- e = Euler's number, a mathematical constant equal to approximately 2.71828