Calculators

Geometry

Solid

Square Pyramid Shape

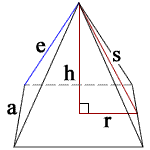
h = height
s = slant height
a = side length
P = perimeter of base
e = lateral edge length
r = a/2
V = volume
L = lateral surface area
B = base surface area
A = total surface area
m = h/r = rise/run = side face slope
θ = tan^-1(h/r) × 180/π = side face angle

Calculator Use

This online calculator will calculate the various properties of a square pyramid given 2 known variables. The square pyramid is a special case of a pyramid where the base is square. It is a regular pyramid since it has a square base which is a regular polygon. This is also a right square pyramid where "right" refers to the fact that the apex lies directly above the centroid of the base. In other words the point at the top of the pyramid is directly above the center point of the square base.

Units: Note that units are shown for convenience but do not affect the calculations. The units are in place to give an indication of the order of the results such as ft, ft² or ft³. For example, if you are starting with mm and you know r and h in mm, your calculations will result with s in mm, V in mm³, L in mm², B in mm² and A in mm².

NAN: means not a number. This will show as a result if you are using values that just do not make sense as reasonable values for a pyramid.

Below are the standard formulas for a pyramid. Calculations are based on algebraic manipulation of these standard formulas.

Square Pyramid Formulas derived in terms of side length = a and height = h:

Volume of a Square Pyramid

• V = (1/3)a²h

Slant Height of a square pyramid

• By the pythagorean theorem we know that
• s² = r² + h²
• since r = a/2
• s² = (1/4)a² + h², and
• s = √(h² + (1/4)a²)
• This is also the height of a triangle side

Lateral Surface Area of a square pyramid (× 4 isosceles triangles)

• For the isosceles triangle Area = (1/2)Base x Height. Our base is side length a and for this calculation our height for the triangle is slant height s. With 4 sides we need to multiply by 4.
• L = 4 x (1/2)as = 2as = 2a√(h² + (1/4)a²)
• Squaring the 2 to get it back inside the radical,
• L = a√(a² + 4h²)

Base Surface Area of a square pyramid (square)

• B = a²

Total Surface Area of a square pyramid

• A = L + B = a² + a√(a² + 4h²))
• A = a(a + √(a² + 4h²))

Slope of Pyramid Side Face

• To find the pyramid slope of the side face we want to calculate the slope of the line s = slant height
• We know that the slope of a line is m = rise/run
• For the line s the rise is h = height of the pyramid
• r = a/2 and this is the run as it forms a right angle where r meets h at the center of the base
• m = h/(a/2) - in terms of h and a
• m = h/r - in terms of h and r

Angle of Pyramid Side Face

• The angle of the pyramid side face is the angle formed between the side face and the base
• Let's name theta θ = Side Face Angle and alpha α = the right angle (90°) formed by h and r
• Using the Law of Sines we can say that s/sin(α) = h/sin(θ)
• Solving for the unknown θ we have
• θ = sin^-1[ (h × sin(α)) / s ]
• We have another formula for θ in terms of the tangent from trigonometric ratios
• Since tan(θ) = side opposite θ / side adjacent θ we can say
• tan(θ) = h/r
• Solving for the unknown θ
• θ = tan^-1(h/r)
• θ in both calculations is in radians. Convert radians to degrees by multiplying θ by 180/π

Square Pyramid Calculations:

Other formulas for calculations are derived from the formulas above.

References

Weisstein, Eric W. "Square Pyramid." From MathWorld--A Wolfram Web Resource. Square Pyramid.